Mathematics of
Quantum Mechanics
(QMath)
The research group "Mathematics of Quantum Mechanics" (Q-MATH) is part of the group "Mathematics Applied to Control, Systems and Signals", which is a research group officially recognized by Universidad Carlos III de Madrid. It is an interdisciplinary research group with many national and international collaborators. It has a wide range of research interests motivated by mathematical and computational questions around quantum theory, including quantum information theory, quantum graphs and quantum field theory. The mathematical techniques used in different projects include, among others, aspects from Linear Algebra, Graph Theory, Operator Theory, Functional Analysis and Group and Groupoid Theory. The group's research has been supported by several national and regional grants over the last ten years. Part of its members are also affiliated to the Instituto de Ciencias Matemáticas (ICMAT, https://www.icmat.es/), a research institute supported by the universities UAM, UC3M, UCM and CSIC which has been distinguished since 2011 as a Severo Ochoa center of excellence. The group organizes a periodic series of seminars (see http://www.q-math.es/).
ENTANGLEMENT AND NONLOCALITY IN QUANTUM THEORY
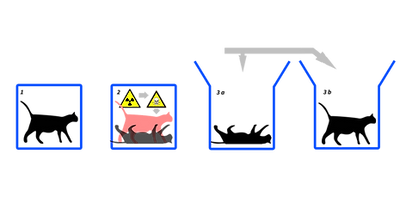
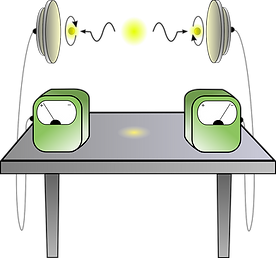
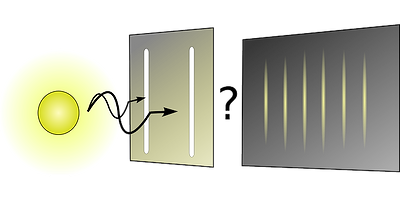
When quantum theory was developed during the first third of the 20th century, its description of reality collided with the hitherto intuition of how a physical theory should be, mainly because of its probabilistic nature. Still, this theory offered excellent agreement with experimental data, so the standard view physicists took (with a few notable exceptions) was to simply use the theory to describe or predict physical phenomena without paying much attention to foundational issues. However, in the last decades this paradigm has changed completely with the advent of quantum technologies. It is precisely the particularities and shocking effects of quantum theory that are at stake with classical intuition what is behind these revolutionary applications such as teleportation, quantum cryptography, randomness generation and quantum computation and simulation. This has shown the necessity for a better understanding of quantum theory and certain parts of its mathematical framework, particularly in the context of information processing, which has led to the development of quantum information theory.
The quantum property with no classical analogue that is at the heart of all these applications is entanglement. This term was coined by E. Schrödinger in 1936 (“Verschränkung” in German) who had the vision to say: “I would not call that one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought”. Entanglement is a property that arises when considering systems composed by two or more subsystems and, loosely speaking, it is a strong form of correlation in the possible outcomes of local measurements by the parties. Later on, in 1964, the existence of entangled states in quantum mechanics allowed J. Bell to prove the incompatibility of this theory with any local realistic theory (i.e. any local hidden variable model) in his celebrated eponymous theorem.
In the modern view of quantum information theory, entanglement is considered as a resource that enables different tasks. Considerable work is devoted to its study in order to classify and quantify the different forms in which it manifests and to devise protocols for its manipulation. Quantum nonlocality emerges as an application of entanglement, which, in addition to its interest for foundational questions, points to particular tasks where quantum set-ups carry an advantage over systems operating under the laws of classical physics.
Projects for both Bachelor and Master’s theses (TFG, TFM) are offered to highly-motivated students to work under the supervision of faculty member Julio de Vicente. Numerical or analytical techniques may be used depending on the student’s background and preferences. Possible topics include:
-
Criteria for entanglement certification.
-
Bell’s theorem, nonlocality in noisy environments and applications.
-
Bell inequalities for genuine multipartite nonlocality and the identification of entangled states that violate them.
-
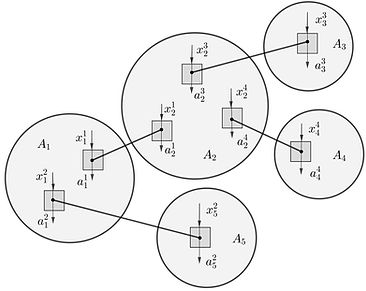
Entanglement and nonlocality in quantum networks.
-
Other quantum-motivated problems:
-
Matrix theory and quantum information (e.g. completely positive maps, generalizations of the rank, quantum states with a particular matrix structure…)
-
Implementation of quantum algorithms in IBM’s Qiskit language.
Contact: Julio de Vicente (jdvicent@math.uc3m.es)
ANALYSIS ON GRAPHS AND QUANTUM FUNCTIONAL ANALYSIS
Projects for both Bachelor and Master’s theses (TFG, TFM) are offered to motivated and ambitious students to work under the supervision of faculty member FERNANDO LLEDÓ. Depending on the mathematical and physical background there are two main areas in which topics may be offered.
-
ANALYSIS ON GRAPHS: Spectral graph theory is a hybrid field that studies the relationship between the structure of a graph and the spectrum of operators naturally associated with it, typically the adjacency and the Laplacian matrices. While the matrices depend on the labeling of the vertices, their spectrum is an invariant that encodes central properties of the graph like the connectedness or the bipartiteness. Numerical quantities like the Cheeger constant provide deep connection to the robustness of the graph and, also, have many surprising applications. In this field also numerical computation of spectra may be implemented for experiments. Possible topics include:
-
Indices of graphs and applications to chemical graph theory.
-
Expander graphs: characterization of sparse and robust graphs.
-
Covering graphs and the Higuchi-Shirai conjecture.
-
-
QUANTUM FUN CTIONAL ANALYSIS: Operators and algebras generated by them and acting on Hilbert spaces is a hybrid field initiated in the 1930s by John von Neumann and developed in close relationship with fundamental aspects from various branches of mathematics including functional analysis, harmonic analysis, and quantum physics. The theory of operator algebras has been since then one of the most pervasive topics both in mathematics and mathematical physics, in particular, in the mathematical description of quantum mechanics and quantum field theory. This field offers a solid mathematical background to address many different approaches to fundamental problems in quantum mechanics. Possible topics include:
-
The spectral theorem and applications to quantum theory.
-
Mathematics of quantum theory. Bounded and unbounded operators.
-
Quantum mechanics and finite dimensional approximations.
-
Algebras of operators generated by the canonical commutation relations (CCR).
-
Contact: Fernando Lledó (flledo@math.uc3m.es)


QUANTUM CONTROL AT THE BOUNDARY


Quantum Information and Quantum Computation are not only a modern expression of Quantum Mechanics and a collection of very promising new technologies, it is also the source of deep and inspiring mathematical problems. We do not have only to ask what Mathematics has to offer to quantum technologies but also what new problems and fields of Mathematics might be opened or enriched due to these important technological challenges. This field of research has the potential to lead to a fruitful exchange of results and ideas between different areas. On one hand contributing to fields of research in pure Mathematics like evolution equations on Banach spaces. On the other hand providing a novel approach to the problem of control of current quantum devices.
Optimal Control Theory on finite dimensional systems has been a fundamental aspect in the development of control techniques in quantum systems. The success of such approaches relies on the fact that the codification of information is done in a finite dimensional subspace of the typically infinite dimensional state space of the system (Hilbert space). This implies that only a finite dimensional subspace is considered in the description of the system. This is an approximation and introduces the problem that one needs to avoid interactions of the system with itself. Interestingly, one effective way of keeping these unwanted interactions under control is considering enlarged spaces, with additional levels, to monitor and control such interactions. The specific approach used changes among different quantum devices and is treated almost on a case by case basis. The theory of infinite dimensional control provides a systematic way of studying such procedures. Moreover, infinite dimensional control techniques can take advantage of the intrinsic infinite dimensional nature of the quantum systems involved and use it as a resource instead of as a drawback. First, addressing the problem as an infinite dimensional problem, will not treat the extra levels, compared with a finite dimensional approximation, as a source of errors or unwanted interactions. More important, this opens the possibility of a completely new type of control technique not considered before. Controlling the state of the quantum system by changing the boundary conditions. This is a completely novel approach with potential applications in many other areas different from Quantum Mechanics.
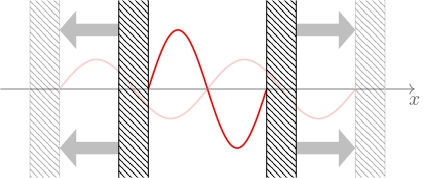
As a concrete setting to develop the above ideas we study quantum graphs. A quantum graph is a graph considered as a one-dimensional variety equipped with a self-adjoint differential (or pseudo-differential) operator. Over each edge of the graph the differential operator acts naturally on the space of functions on that edge. The graph structure becomes apparent to the differential operator when imposing the boundary conditions at the vertices of the graph. From a more mathematical perspective this becomes the problem of analysing the self-adjoint extensions of the corresponding differential operators. Quantum graphs are effective simplified models for situations where one propagates waves of different nature through quasi-one-dimensional systems, i.e. that look like thin neighbourhoods of graphs. For instance, electron propagation in certain molecules (graphene), quantum wires, photonic crystals or scattering theory.
There are several possible topics to work in the context of Quantum Control at the boundary depending on the students preference.
-
Numerical Methods for Optimal Control of Evolution of Quantum States: Improving current quantum computation schemes.
-
Optimal Control of Evolution of Quantum States: Analytical Aspects.
-
Modelling Superconducting Circuits with boundary conditions: Towards high fidelity models for Superconducting Q-bits
-
Other topics related with the above but not listed here are also possible.
Contact: Juan Manuel Pérez Pardo (jmppardo@math.uc3m.es)
CLASSICAL AND QUANTUM INFORMATION GEOMETRY
Information geometry is a multidisciplinary research field encompassing various topics such as classical and quantum information theory, classical and quantum metrology, machine learning, statistical decision theory, and statistical data analysis.
In classical information geometry, the focus is on manifold of probability distributions, the so-called statistical models (like normal distributions, Poisson distributions, and gamma distributions). It turns out there is a rich geometrical structure on these manifolds which is encoded in two tensor fields: the Fisher-Rao metric tensor, and the Amari-Čencov skewness tensor. The resulting geometry provides insights into statistical inference, machine learning, and information theory, by means of the Cramér-Rao inequality for unbiased estimators, the natural gradient algorithm for statistical learning, the generalized Pythagorean theorem and its relation to maximum likelihood estimator in exponential models, the EM and em algorithm for neural networks, to cite just a few examples.
Quantum information geometry extends these concepts to the realm of quantum mechanics, where, instead of probability distributions, the fundamental objects are quantum states (represented by density operators on the Hilbert space of the system). The geometry of the space of quantum states is more complex due to the non-commutativity of quantum mechanical observables. For instance, both the Fisher-Rao metric tensor and the Amari-Čencov skewness tensor have infinitely-many quantum generalizations, and different geometries must be used for different information-theoretical tasks. Moreover, the peculiar character of quantum entanglement leads to non-classical correlations whose geometrical and topological characterizations present one of the most interesting open problems of quantum information geometry.
Projects for both Bachelor and Master’s theses (TFG, TFM) are offered to highly-motivated students to work under the supervision of Dr. Florio M. Ciaglia. Depending on the student’s background and preferences, possible topics include (but are not limited to):
1) divergences, relative entropies, and information geometry of classical and quantum systems;
2) geometrical aspects of classical and quantum estimation theory and metrology;
3) dual connections and exponential models in classical and quantum information geometry; 4) algebraic formulation of classical and quantum information theory in finite dimensions.
Contact: Florio Ciaglia (fciaglia@math.uc3m.es)