GISC - Research topics in theoretical biology, evolution and related subjects


Biological evolution
BIOLOGICAL EVOLUTION AND GENOTYPE-PHENOTYPE MAP
Populations of living organisms are made up of individuals that vary in their genetic information, what we know as genotype. Each genotype translates into a series of observable characteristics, known as phenotype. Classical models of evolutionary theory assume that individuals reproduce more or less effectively according to their phenotype, and in the reproductive process they undergo mutations so that the offspring does not have exactly the same genotype as their parents.
Recent work has explored the evolutionary dynamics of genotype spaces on which a network structure is imposed, in which genotypes are the nodes of the network and mutations are links between nodes
(Aguirre et al. 2018, Manrubia et al. 2021). These studies have shown that the network structure of genotype space fundamentally alters the predictions of evolutionary models.
Our research line is thus focused on studying evolutionary dynamics on genotype networks from a computational perspective. The following research projects are offered:
1) EVOLUTION SIMULATOR
The project will consist of developing an agent-based evolution simulator that implements population dynamics in toyLIFE, (Catalán et al. 2018, 2020), a computational model which includes organisms with ``toy'' versions of genes, proteins and metabolites. The simulator will attempt to replicate real experimental designs used in evolutionary experiments with bacteria, so that the results of the simulations can be compared with published experiments.
2) EXIT TIMES FROM A PHENOTYPE
The objective of this project is to study the distribution of transition times between phenotypes in the computational model toyLIFE (Catalán et al. 2020), so that we can delve into the effects that the network structure at the genotype level has on phenotypic dynamics.
3) EVOLUTION IN ALTERNATING ENVIRONMENTS
Numerical simulations of populations evolving in networks of genotypes under alternating antibiotic treatment show that populations can get stuck in regions of these genotype networks where they cannot evolve resistance to new antibiotics (Catalán et al. 2017). The aim of this project is to simulate the evolution of several populations under alternating environments. To do this, we will take as a starting point a recent work by Kevin Wood's group (Maltas et al. 2021) and we will implement the appropriate population dynamics to study this phenomenon.
REFERENCES
Aguirre, J., Catalán, P., Cuesta, J.A. and Manrubia, S. On the networked architecture of genotype spaces and its critical effects on molecular evolution. Open Biol. 8, 180069 (2018).
Catalán, P. Models in molecular evolution: the case of toyLIFE. Tesis doctoral, Universidad Carlos III De Madrid (2017).
Catalán, P., Wagner, A., Manrubia, S. and Cuesta, J.A. Adding levels of complexity enhances robustness and evolvability in a multilevel genotype–phenotype map. J. Roy. Soc. Interface 15, 2017051617 (2018).
Catalán, P., Manrubia, S. and Cuesta, J.A. Populations of genetic circuits are unable to find the fittest solution in a multilevel genotype--phenotype map. J. Roy. Soc. Interface 17, 20190843 (2020).
Maltas, J., McNally, D.M and Wood, K.B. Evolution in alternating environments with tunable interlandscape correlations. Evolution 75, 10--24 (2021).
Manrubia, S. and Cuesta, J.A. Evolution on neutral networks accelerates the ticking rate of the molecular clock. J. Roy. Soc. Interface 12, 20141010 (2015).
Manrubia, S., Cuesta, J.A. et al. From genotypes to organisms: State-of-the-art and perspectives of a cornerstone in evolutionary dynamics. Phys. Life Rev. 38, 55-106 (2021).
Web: https://pablocatalan.github.io
Twitter: @the100footpole
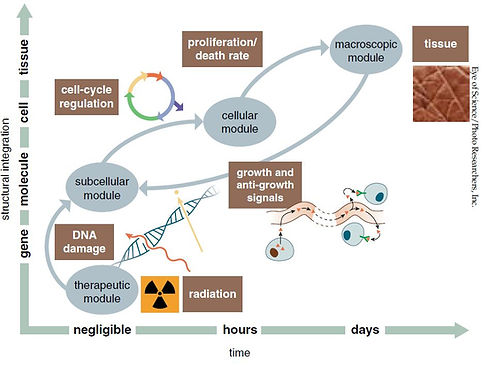
Cancer modelization
Understanding the behavior and growth of diseases such as cancer is important and establishes a whole area of research with many aspects yet to be understood. Tumor is composed of a heterogeneous population of cells and whose growth is rapid. Spatial organization of the tumor cells, understand the mechanisms that coordinate growth and patterning of tissues. These processes occur as a result of cell adhesion, migration, division, differentiation and death, and involve multiple processes acting at the cellular and molecular level. We study this phenomena by developing a systems biology mathematical framework employing analytical and computational tools that make use of dynamical systems, stochastic processes, and Bayesian inference.